之前使用matlab模拟本征值的链接如下:
现在使用bout3中的slepc求解器尝试对这一问题重复操作:
int rhs(BoutReal t) {
mesh->communicate(u, v);
// First-order system:
// du/dt = v
ddt(u) = v;
// dv/dt = -[M]^{-1}[K]u
// Euler-Bernoulli beam equation: EI * d⁴u/dx⁴ + ρA * d²u/dt² = 0
// So dv/dt = -(EI/ρA) * d⁴u/dx⁴
// Compute fourth derivative using D2DX2 twice
// First apply d²u/dx²
Field3D d2u = D2DX2(u);
d2u.applyBoundary("neumann"); // Apply boundary conditions for stability
mesh->communicate(d2u);
// Then apply d²/dx² again to get d⁴u/dx⁴
Field3D d4u = D2DX2(d2u);
d4u.applyBoundary("neumann");
mesh->communicate(d4u);
// dv/dt = -(EI/ρA) * d⁴u/dx⁴
BoutReal coeff = -(E * I) / (rho * A);
ddt(v) = coeff * d4u;
// Apply boundary conditions to ddt(v) to avoid non-finite values at boundaries
ddt(v).applyBoundary("dirichlet");
return 0;
}
输入模块BOUT.inp中与solver相关的内容如下:
[solver]
type = "slepc"
neig = 64
mpd = 128
useInitial=true
maxit=10000
tol=1.0e-4
userWhich = false
targRe=0.0
targIm=0.0
selfSolve = false
timestep = 0.01
# Matrix output options for debugging
outputMatrix = true
matrixOutputRows = 20
matrixOutputFile = true
# Eigenvector output options
outputEigenvectors = true
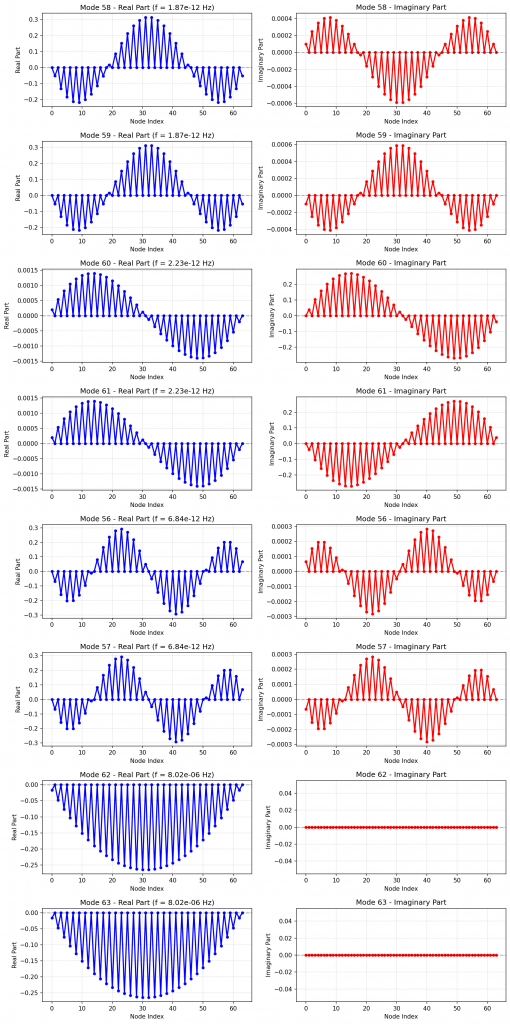
numEigenvectorsOutput = 8与之前文章不同的是,这次两边的边界条件都是neumann,从而导致两边固定,第一个本征值应该为0。运行结果如下:
Eigenvector 57 saved to data/eigenvector_57.txt
58 -1.17483e-11+5.29770e+02i (529.77) -5.29770e+02-1.17483e-11i (529.77)
Option :datadir = data
Eigenvector 58 saved to data/eigenvector_58.txt
59 -1.17483e-11-5.29770e+02i (529.77) 5.29770e+02-1.17483e-11i (529.77)
Option :datadir = data
Eigenvector 59 saved to data/eigenvector_59.txt
60 -1.40204e-11+1.93112e+02i (193.112) -1.93112e+02-1.40204e-11i (193.112)
Option :datadir = data
Eigenvector 60 saved to data/eigenvector_60.txt
61 -1.40204e-11-1.93112e+02i (193.112) 1.93112e+02-1.40204e-11i (193.112)
Option :datadir = data
Eigenvector 61 saved to data/eigenvector_61.txt
62 5.04113e-05+0.00000e+00i (5.04113e-05) 0.00000e+00+5.04113e-05i (5.04113e-05)
Option :datadir = data
Eigenvector 62 saved to data/eigenvector_62.txt
63 -5.04113e-05+0.00000e+00i (5.04113e-05) 0.00000e+00-5.04113e-05i (5.04113e-05)
Option :datadir = data
Eigenvector 63 saved to data/eigenvector_63.txt
可以看到第一个本征值为0,第二个本征值为193,第三个本征值为529,与之前文章中的30,191,534,基本吻合。