文章信息 [1]

• 作者：Chaotong Yang, Kai Li, Guoqiang Li
• 期刊：nature scientific reports
• 机构：青岛大学，等离子体物理研究所，中国科学技术大学
• 时间：2025年5月

---

摘要

托卡马克等离子体的物理过程里，芯部和边界物理的耦合很重要，是未来燃烧等离子体的关键物理基础，本文章在REPED预测type 1 ELM的基础上，进一步用在 type 3 ELM上。同时还结合了TGYRO输运模块，在芯部和边界物理耦合上预测得到剖面并且与实验相验证。

---

背景

芯部和边界对于托卡马可都很重要，尤其是在理解H模的等离子体放电行为上。

• PB模能够影响全局的Shafranov位移
• EPED结合PBM与KBM给出台基结构判据
• 约束和输运有多个影响因素
  • 等离子体平衡
  • 密度温度剖面
  • 加热和粒子源

因此研究芯部与台基耦合的输运过程能有助于理解托卡马克H模台基和芯部物理。

---

目前在DIII-D上预测剖面使用最多的主要是EPED模型和TGYRO输运模型，并取得了较好的实验一致性。EAST上也有类似的流程，但是存在一些问题：

• 使用TGYRO输运模型时通常使用的是实验获得的固定剖面
• 通常在预测台基的基础上采用一个简单的函数来得到芯部的参数，忽略芯部的峰值
• 诊断数据不可靠

因此，如何快速高效地预测H模的剖面很重要。

---

本文结合REPED模型和TGYRO输运模型预测EAST的H模的台基。

REPED已经成功运用在Type 1ELM的预测。

$$
\Delta_\psi = 0.12 \beta^{1/2}_\text{p,ped}
$$

尽管type III ELM可能收到阻性气球模的影响，但REPED可能也能适用，并且在芯部的剖面部分，采用TGYRO来计算输运系数。

---

REPED在Type III ELM的验证

数据来源

plasma parameters
Shot	102187	80678	69033	54863	543845
Time (ms)	7700	4910	3950	3650	3450
Plasma current $I_p$ (kA)	450	415	460	460	460
Line-average density $\qty(n_e)\qty(10^{19} m^{-3})$	5.33	3.78	5.64	5.47	3.84
Plasma Stored energy $W$ (MJ)	1.73	1.26	1.55	1.40	1.43
Normalized toroidal beta $\beta_N$	1.14	1.31	0.91	1.19	1.21
Poloidal beta $\beta_p$	1.15	0.98	0.99	0.91	0.92
Toroidal magnetic field $B_T$ \qty(T)	2.43	1.63	2.48	1.67	1.68
Power of NBI $P_\text{NBI} \qty(MW)$	2.6	2.2	6.2	2.5	2.4
Power of LHW $P_\text{LHW} \qty(MW)$	1.8	0.8	3.0	1.2	2.0

过去几年对type III ELM的研究所得到的数据正好用来验证这次的模拟模型。

---

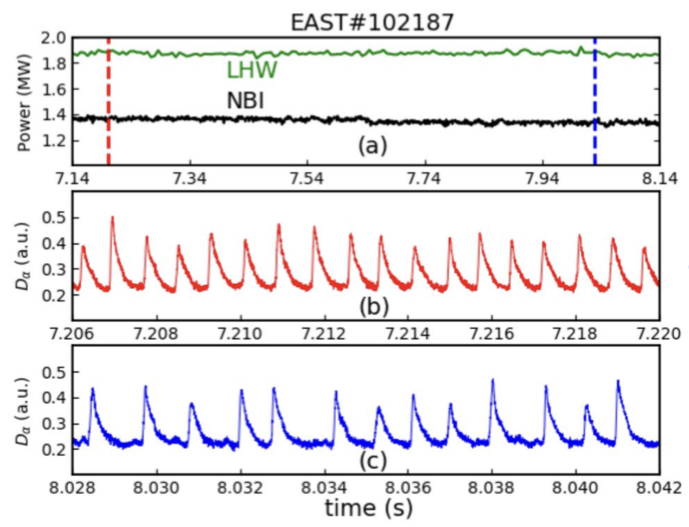
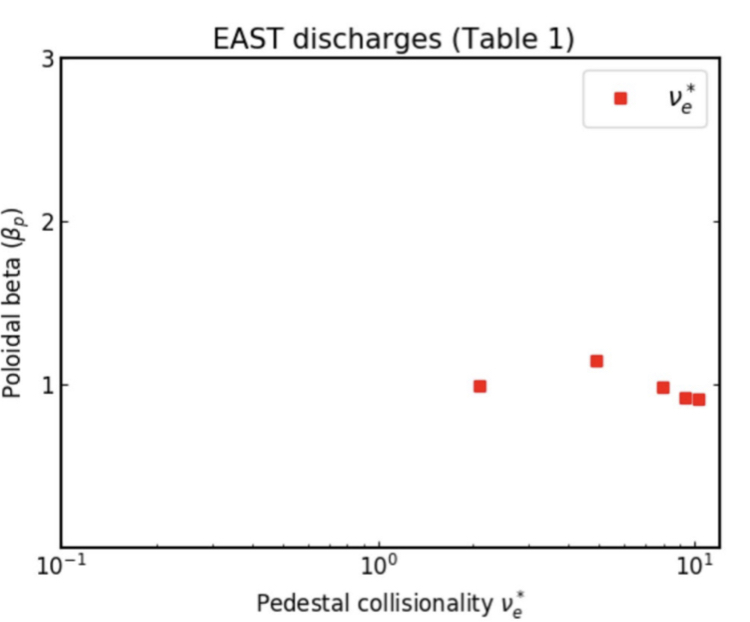
通过对特定数据的参数分析来得到这一系列ELM属于type III ELM的结论。

---

REPED与EPED的区别

模型	EPED	REPED
平衡程序	TOQ	TEQ

其中TOQ仅支持上下对称的平衡位型，而TEQ支持的位型更多。

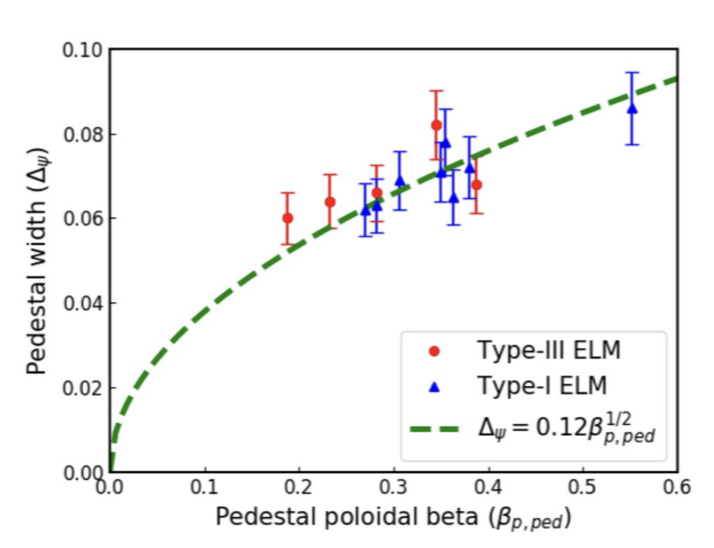
宽度模型$\Delta_\psi = 0.12 \beta^{1/2}_\text{p,ped}$在EAST上面在type I与type III的ELM上均得到了验证。

---

工作流

用EPED/ELITE来预测PBM模的稳定性边界的工作流的细节如下：

使用TEQ平衡求解器构建一系列平衡，这些平衡被输入到ELITE的代码中，为了构建这些平衡需要如下参数。

• 压强$p$

$p = n_e T_e + \qty(n_i + n_z) T_i$，模型近似$T_i = T_e$

• 离子密度$n_i$和杂质密度$n_z$，

通过准中性和$Z_\text{eff}$获得

• 有效核电荷数$Z_\text{eff}$

通过实验数据测量整个小半径的数据得到，$Z_\text{eff}$通过带状电流（bootstrap current）和核心输运模型（通过稀释特性dilution effect）来影响台基模型。

• 电子密度$n_e$与电子温度$T_e$

通过下面的公式直接得到

\begin{equation}
\begin{aligned}
n_e\qty(\psi) = n_\text{sep}
& + a_{n0}
\qty{\tanh\qty[\frac{2\qty(1 – \psi_\text{mid})}{\Delta_\psi}]
– \tanh\qty[\frac{2\qty(\psi – \psi_\text{mid})}{\Delta_\psi}]}\\
& + a_{n1} H\qty(1-\frac{\psi}{\psi_\text{ped}})
\qty[1 – \qty(\frac{\psi}{\psi_\text{ped}})^{\alpha_{n1}}]^{\alpha_{n2}}\\
T_e\qty(\psi) = T_\text{sep}
& + a_{T0}
\qty{\tanh\qty[\frac{2\qty(1 – \psi_\text{mid})}{\Delta_\psi}]
– \tanh\qty[\frac{2\qty(\psi – \psi_\text{mid})}{\Delta_\psi}]}\\
& + a_{T1} H\qty(1-\frac{\psi}{\psi_\text{ped}})
\qty[1 – \qty(\frac{\psi}{\psi_\text{ped}})^{\alpha_{T1}}]^{\alpha_{T2}}\\
\end{aligned}
\end{equation}

此时可以将EAST的参数代入到模拟中，比如$n_\text{sep} = n_\text{e, ped}/4, T_\text{sep} = 50eV, a_{n0} = 1.0, \alpha_{n1} = 0.9, \alpha{n2} = 1.8, \alpha_{T1} = 1.2, \alpha_{T2} = 1.4$

接下来通过如下几步确定参数细节：

• 通过<ne>和密度峰值来约束$n_e$，调节$a_{T1}$来维持$\beta_N$（在特定的$T_e$下）。
• 扫描不同的台基高度和台基宽度来得到不同的台基剖面。
• 通过计算Sauter bootstrap current模型在计算电流剖面。
• 通过简单的函数来拟合出核心的电流剖面，保证总电流相同。
• 通过扫描不同的$a_{T0}$来过的不同的平衡。
• 基于这些平衡，跑ELITE程序得到$n = 5-30$的PBM稳定性。
• 得到PBM的稳定边界。

---

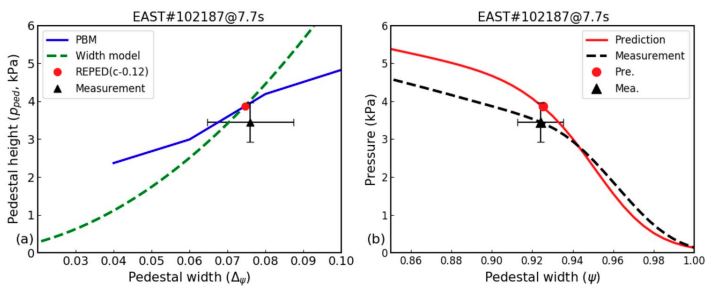
上图展示了REPED模型在type-III ELMs的H模上预测台基结构的可行性。

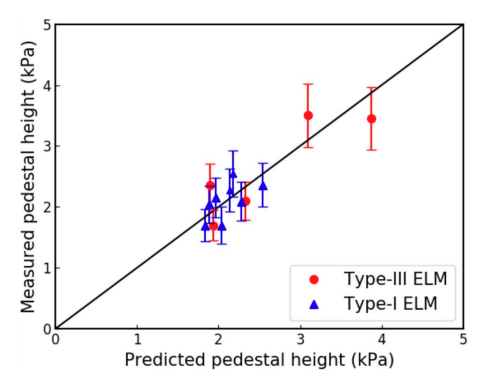
上图展示了REPED模型既可以用于预测EAST的一类ELM下的台基结构，也可以用于预测三类ELM下的台基结构。

在EAST模拟上使用核心-台基耦合的综合模拟

类似OMFIT，我们将其中的EPED模型替换为REPED模型来得到对EAST H模核心-台基耦合的模拟结果。

结构说明

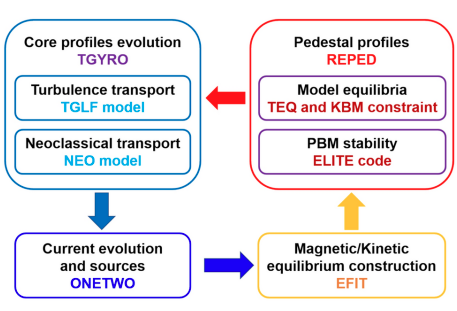
上图中，EFIT模块作为初始平衡构建和输入；TGYRO用来计算粒子和能量的输运流（通过调用湍流输运代码TGLF和新经典输运代码NEO），来得到稳态的密度温度剖面；ONETWO输运模型用来计算粒子和能量的源。

---

流程说明

1. 从实验数据出发，运行EFIT得到初始时刻的平衡和主要参数。然后运行REPED模型预测到台基结构，其中TEQ代码构建初始的动理学剖面（$n_e, T_e, T_i = T_e$）。
2. 初始动理学剖面放到GENRAY和CQL-3D得到LHW的计算，然后使用ONETWO输运模型得到能量和粒子的源。
3. 平衡和源都被输入到TGYRO代码中。
   • 开始固定$n_e$来演化$T_e, T_i$
   • 然后固定温度基本不变来演化$n_e$
   • 最后得到$\rho = 0.2-0.8$的动理学剖面
4. EFIT代码被再次运行，输入动理学剖面，更新得到新的平衡。
5. 重复第2步到第4步，直到剖面基本不再变化。

---

模拟结果分析

下图左侧是对EAST放电56924做模拟实验的比照，缺少$T_i$的数据；右侧是对EAST放电102187的模拟实验的比照，含有较多的Ar杂质。

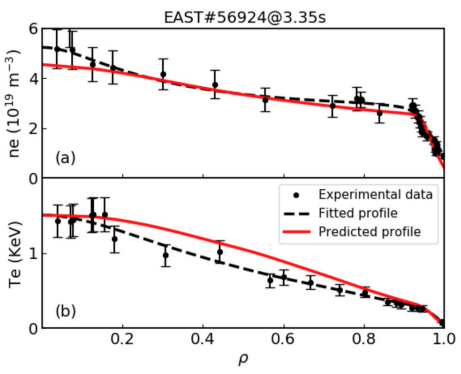
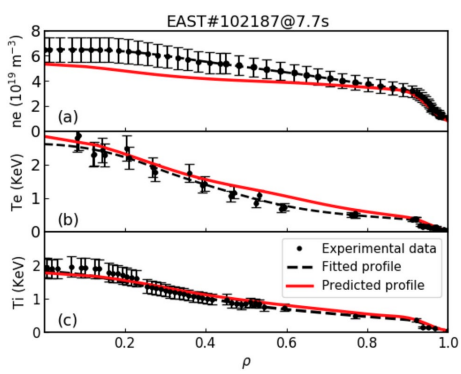
分析上面可以看出预测和诊断的数据符合得比较好，分析有差异的地方得到如下几个结论：

• 杂质导致核心$n_e$较高（由于杂质的电离）
• 诊断的误差和限制导致一定的偏差
• 只能测出平均的$Z_\text{eff}$，模型中只好假设$Z_\text{eff}$全部是平的

总结

通过结合REPED与TGYRO可以从边界到芯部研究EAST的H模的剖面。虽然边界本应用阻性磁流体来研究type-III ELM，但是基于理想等离子体的预测也效果还不错。这个综合的模拟可以极大提高实时预测的能力，来服务其他物理研究。

未来的方向包括以下内容：

• 建立更大的数据库
• 研究杂志对于芯部$n_e$的误差
• 目前存在的一些误差，可能是诊断的误差
• $Z_eff$被假定是平的，不够合理，需要进一步研究
• 提高适用性和泛用性（其他不同的放电条件）