文章信息 [1]

• 作者：A. Ishizawa, Y kishimoto, Y Nakamura
• 期刊：Plasma Physics and Controlled Fusion
• 机构：Graduate School of Energe Science, Kyoto University
• 时间：2019年五月

摘要

带状流（zonal flow）比较弱时，一些大尺度结构如磁岛开始变得重要；通过多尺度交互，大尺度模主导湍流结构，小尺度模进一步影响大尺度结构；这种多尺度相互作用可以根据撕裂模（Tearing Mode/TM）的稳定性来分类。

• 当TM不稳定，磁岛宽，湍流磁岛分割处增强，从而形成陡峭温度梯度，与带状流的剪切相对应。
• 当TM接近稳定时，湍流输运主导，磁岛宽度在拉莫尔半径整数倍。这时的磁岛被称为新经典撕裂模的种子磁岛（seed-island）

此时扰动的对称性起了关键作用。

• 磁岛属于撕裂对称模
• 漂移波不稳定性属于扭曲对称模

背景

湍流主要是由漂移不稳定模如ITG和TEM驱动，进一步形成带状流(zonal flow)，在低$\beta$下调控湍流输运，而当$\beta$升高后，湍流扰动呈现电磁特性，从而激发KBM。

此时的电磁特性激发长波MHD不稳定性，如撕裂模（TM）。这时会重新形成闭合磁面并降低约束性能。此时带状流（zonal flow）会变弱，湍流导致带状结构向相干结构(coherent structure)转变。部分磁岛会由长波数与带状磁场、带状压强共同主导。

磁岛

如下面的截面所示，磁岛围绕一个O点，该处的磁场消失。另一个磁场消失的点为X点。穿过X点的面称为磁岛的分截面。因此磁岛的形成导致温度/密度的分布平坦化，导致约束性能降低，比如ElMy H模。更进一步，当一串磁岛出现在各个半径，并且互相堆叠时，约束性能进一步降低以致于破裂，这是因为堆叠的磁岛会在广泛的范围内形成随机磁岛。

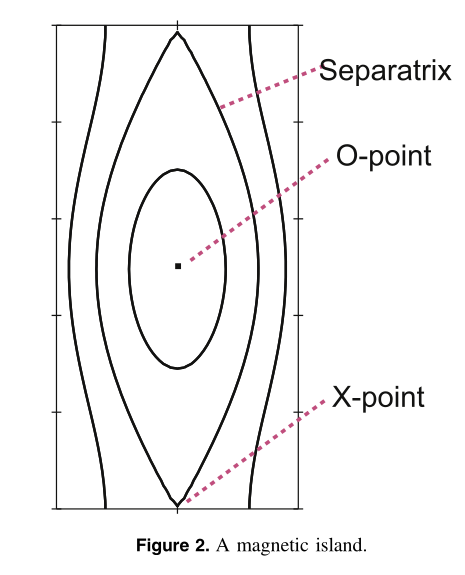
当等离子体被层层磁场约束起来的时候，磁重联现象改变了磁场线的拓扑，从而形成磁岛。X点就是磁重联发生的地点。磁岛是由撕裂模引起的，是一种自发的磁重联。而新经典撕裂模（NTM）是由磁岛分离面内的压强梯度降低引起的自举电流（bootstrap current）触发的，因此新经典撕裂模会在有限尺寸的磁岛中超过阈值而涨起来。这种“种子磁岛“（seed magnetic island）的尺度是整数倍的拉莫尔半径（实验测得）。这种种子磁岛也可以由外部触发，如锯齿模（sawtooth crash）和边界局域模（ ELMs）等。

比如$(m,n)=(1,1)$的锯齿模扰动激发一个在 $q=1$的有理面上$(m,n) = (2, 2)$的高阶谐波（higher harmonics），从而产生一个$(m, n) = (3, 2)$的磁场扰动，生成种子磁岛，进一步激发一个$q=3/2$的NTM。另一方面根据JT-60U的实验观测，就算没有任何锯齿模和ELMs，$(m,n) = (2, 1)$的NTM依然能被观测到，因此电磁漂移波扰动(electromagnetic drift-wave turbulence)可作为该实验的解释。

磁岛也可以由有理面的外部磁扰动（RMP）所激发。RMPs将会用在ITER上用于控制ELMs，扰动闭合磁面并形成$E \times B$流，形成电磁漂移波扰动从而形成磁岛结构。

湍流和相干模的非线性相互作用是理解等离子体约束降低的一个关键，因为漂移波湍流在磁约束等离子体中普遍存在，并和磁岛非线性耦合。

事实上在JT60U的反剪切位形等离子体破裂前，观察到低波数的MHD活动，其中观测到一个与带状流和和漂移波湍流相关的输运垒。进一步LHD等离子体中也观测到微湍流。从下图揭示了湍流和磁岛之间的相互关系的各个尺度。

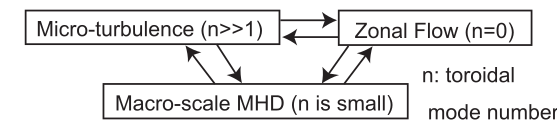
其中由漂移不稳定性引起的通常是高n扰动，而撕裂模引起的磁岛多为低N,如下图所示。

高波数压强驱动的不稳定性和低波数电流驱动的不稳定性之间的相互影响。关于湍流和磁岛的理论研究目前主要集中于湍流给撕裂模带来的异常电阻，异常电子粘滞，和湍流引起的负粘滞等等。而两者的相互影响主要通过磁流体模型和动理学模型的数值模拟来研究，本文章会作一定的介绍。

文章构成

由于磁岛是由于撕裂模引起的，这是一种长波不稳定性，主要由平衡电流梯度驱动，因此可以分为两个情况进行讨论。

• TM不稳定
  • 磁岛半径远远大于拉莫尔半径$W \gg \rho_i$，在section 4讨论
• TM稳定或亚稳定
  • 磁岛半径远远大于拉莫尔半径$W \geqslant \rho_i$，在section 5讨论

在Section 6进一步讨论静态磁场和湍流与极向电流的相互作用。

KSTAR、DIII-D、EAST、HL-2A的实验都有研究相关问题，同时与数值模拟的对比研究才刚刚开展，各种多尺度的相关作用（包括GAM、zonal flow、磁岛、湍流）使用双流体模型模拟在简化位形（柱，环等）下也有一定的研究。

Section 4还介绍了当TM不稳定时，引发大磁岛，然后磁岛通过磁场扰动形成的相干涡流导致压强梯度减小，进一步影响湍流。

• Section 4.1：但实验和模拟都观测到磁岛分离面内温度和密度剖面的梯度减小是不完整的，由于湍流在分离面内部的原因。
• Section 4.2：分离面内的湍流输运增强是由湍流和磁岛共同作用导致的。
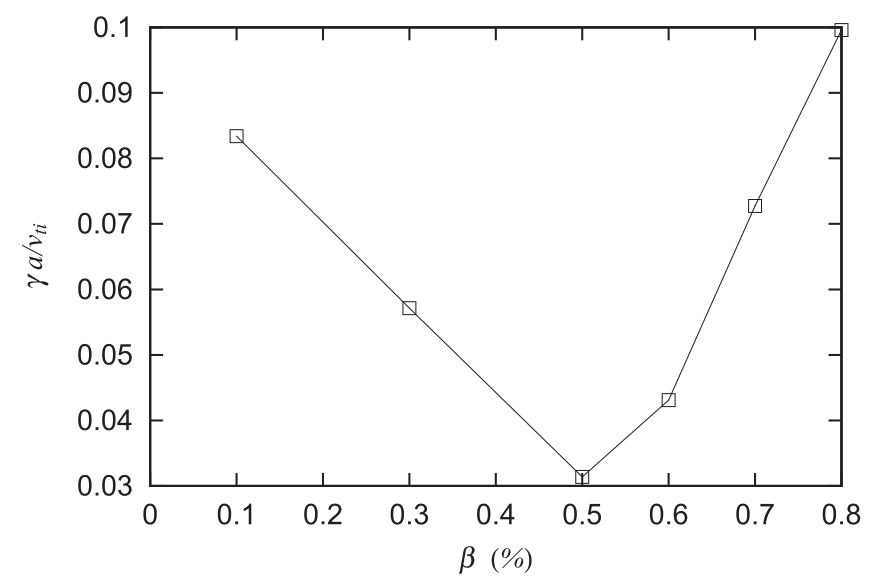
• Section 4.3：通量模拟和非通量模拟对极向角湍流强度的影响不一样，通量较弱，非通量较强。同时有限$\beta$的带状流强度低，进一步导致磁岛对于流动的改变。磁岛引起带状流的震荡。
• Section 4.4：磁力线在环向变得混乱，X点对于磁扰动变得敏感。因此湍流的磁涨落使得磁场进一步变得混乱，尤其是X点附近。
• Section 4.5：湍流主要影响磁岛还很小并且在增长的时候，其增长主要由湍流异常电阻增强的。

Section 5介绍了当TM稳定时，湍流产生长波磁岛，由于湍流涨落在有限$\beta$下的电磁特性，此时磁岛宽度与拉莫尔半径相当$W \geqslant \rho_i$。这与NTMs的出发机制相似，从而限制了托卡马克等离子体的$\beta$提高。因为就算TM稳定，湍流依然会形成种子磁岛。然而此时湍流形成磁岛的过程并不简单：大尺度相干模式与小尺度的湍流广泛存在，大量的模会被触发（并不代表磁岛会被触发）。磁岛似乎只在上发生磁重联时，且在低的$(m,n)$有理面，磁场弯曲稳定效应不明显的地方才会被触发。因此，磁岛的形成不仅需要能量向相干模式转移，还需要对称混合和磁场重联。

Section 6讲除了TM稳定性分类来研究，还可以在静态磁岛模型的基础上研究湍流。因为极化电流效应（磁岛增长的一个重要机制）可以由静态磁岛模型来计算。由湍流导致的极化电流首先使用静电交换模（ICs）来进行数值模拟，后来在ITG湍流的模拟中进一步研究。研究发现湍流导致的极化电流确实能引发磁岛。

行文总结

• section 2: 数值模拟中的双流体模型的介绍
• section 3: Parity的介绍
• section 4: TM不稳定时的相干模拟
• section 5: TM稳定时的相干性和parity对称性的重要性。
• section 6: 静态磁岛模型的介绍
• section 7: 总结

模型方程

这里介绍数值模拟中使用的双流体方程。大多数研究湍流和磁岛的流体模型都是下面五场双流体方程的子集。

---

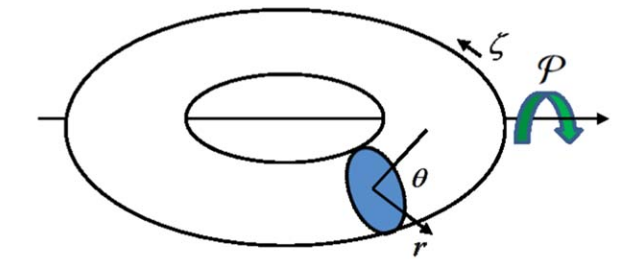
环位形的流体模型

我们首先考虑三场环位形等离子体，使用标准简化(reduced)双流体方程的一个扩展，添加了离子温度和朗道流体效应（Landau fluid closure）。该模型如下内容组成：

• 静电势$\phi$的涡量方程
• 电子密度$n$的方程
• 平行速度$\nu_\parallel$方程
• 欧姆定律的磁通$\psi$方程
• 离子温度$T_i$的方程。

---

方程如下：

\begin{equation}\label{eq:2_1_phi}
n_\text{eq} \frac{D\nabla^2_\perp \phi}{Dt} =
– \nabla_\parallel J – K \qty[p]
+ \tilde a \nabla_\perp \cdot \qty[\nabla_\perp \phi, p_i]
+ \mu \nabla^2_\perp \nabla^2_\perp \phi
\end{equation}

\begin{equation}\label{eq:2_1_n}
\frac{Dn}{Dt}=
– n_\text{eq} \nabla_\parallel \nu_{e\parallel}
+ K \qty[n_\text{eq} \phi – p_e]
+ \mu \nabla^2_\perp n
\end{equation}

\begin{equation}\label{eq:2_1_nu}
n_\text{eq}\frac{D \nu_\parallel}{D t} =
– \nabla_\parallel p + \mu \nabla^2_\perp \nu_\parallel
\end{equation}

\begin{equation}\label{eq:2_1_psi}
\beta \pdv{\psi}{t} =
-\nabla_\parallel \phi
+ \frac{1}{n_\text{eq}} \nabla_{\parallel} p_e
+ \eta_L \nu_{e\parallel}
+ \eta J
\end{equation}

\begin{equation}\label{eq:2_1_t}
\begin{aligned}
\frac{D T_i}{Dt}=&
-\qty(\gamma – 1)\qty(T_\text{eq}\nabla_\parallel \nu_\parallel + \kappa_L T_i) \\
& + T_\text{eq}K\qty[\qty(\gamma – 1)
\qty(\phi + T_i + T_\text{eq} n / n_\text{eq})
+ \gamma T_i]
+ \mu \nabla^2_\perp T_i
\end{aligned}
\end{equation}

其中方程里有如下规定：

\begin{equation}
\begin{aligned}
\frac{D f}{D t} =& \pdv{f}{t} + \tilde{a} \qty[\phi, f] \\
\nabla_\parallel f =& \epsilon \pdv{f}{\zeta} – \beta \tilde{a}\qty[\phi, f] \\
K\qty[f] =& 2 \epsilon \qty[r \cos \theta, f] \\
\qty[f, g] =& \pdv{f}{r} \frac{1}{r} \pdv{g}{\theta} – \frac{1}{r} \pdv{f}{\theta} \pdv{g}{r} \\
\eta_L =& \sqrt{\frac{\pi}{2} \tau \frac{m_e}{m_i}} \vqty{\nabla_\parallel} \\
\kappa_L =& \sqrt{\frac{8T_\text{eq}}{\pi}}\vqty{\nabla_\parallel}
\end{aligned}
\end{equation}

另外还有拉莫尔半径$\rho_i$、小半径大半径比$\epsilon = a/R$、大半径$R$、小半径$a$、热力学系数$\gamma = 5/3$、拉莫尔半径倒数$\tilde a = 1/\rho_* = a/\rho_i$。在这些方程里面

二维模拟的流体模型

对称性（Parity）

我们讨论磁化等离子体中扰动的对称性，并且考虑两种对称性：一种反应了径向方向等离子体的平行对称。另一种反应沿着磁场线时的对称性。我们先讨论第一种再讨论第二种。

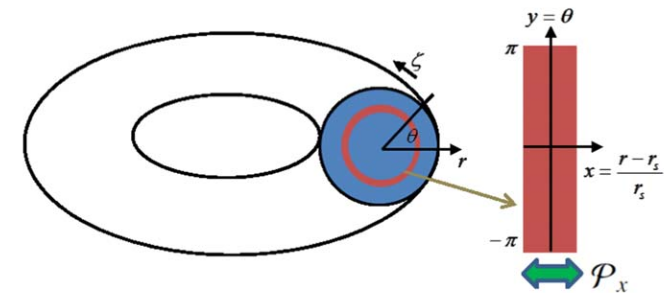
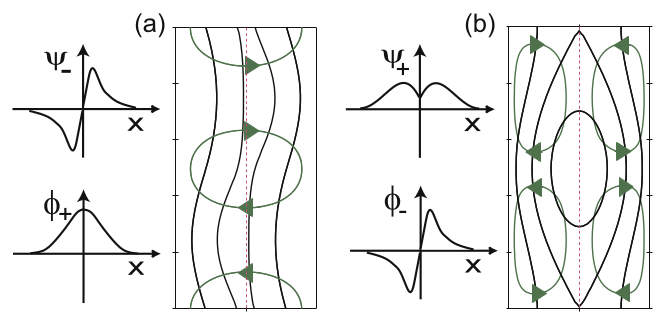
径向的对称性

我们考虑一个有理面的径向对称性的时候。这是一个reduced MHD模型的两场模型到五场的扩展。上图展示了静电势$\phi$和扰动磁通$\psi$分别在扭曲对称性和撕裂对称性中的体现。

• $\psi$为偶对称，$\phi$为奇对称则为扭曲膜。$E \cross B$流扭曲磁面但不改变拓扑。
• 撕裂膜阻止导向X点的$E \cross B$流。

沿着磁力线的对称性

不稳定TM

由磁通驱动的撕裂模电磁扰动

相干涡流

带状流

随机磁场

反常电流驱动

非磁通模拟

稳定TM

由湍流驱动的磁岛

磁岛的演化

非线性对称性混合

直接非线性对称性混合

调制对称不稳定性

静态磁岛模型

湍流导致的极化电流

强制演化

自由演化磁岛

磁岛对湍流的影响

总结

本文章回顾了小尺度湍流一直到大尺度的磁岛的非线性相互作用。这对理解有限$\beta$等离子体中的湍流输运与电磁涨落非常重要。

多尺度非线性相互作用可激发长波相干扰动（低m,n），但这并不代表产生相干磁岛。磁岛仅当相干模具有撕裂对称性和磁重联发生在中性/有理平面。所以，这个多尺度相互作用是一个自发的磁重联，可以有TM的稳定性参数$\Delta^{‘}$来判定。

利用线性电阻MHD撕裂莫理论，$\Delta > 0$表示磁岛的形成，由此来判断有限磁岛的产生。与此同时，湍流一定程度影响了这个判据阈值：

1. 撕裂模不稳定时，激发的扰动存在撕裂对称性，并且磁岛半径远大于拉莫尔半径$W \gg \rho_i$，从而释放平衡电流密度梯度中储存的自由能。
2. 撕裂模稳定时，一部分湍流激发存在撕裂莫对称性，从而在有理共振面新城磁岛，此时磁岛宽度大概在5倍的拉莫尔半径$W \approx 5 \rho_i$

首先我们总结第一个，然后我们解释第二个。

---

TM不稳定时

此时湍流和磁岛的相互作用，主导了湍流扰动。就算在TM的增长率很低时，甚至低于漂移波不稳定性。

$$\gamma_\text{TM} \ll \gamma_\text{drift-wave}$$

在多尺度相互作用下，磁岛破坏气球模结构并拓宽湍流谱，形成相干涡流，从而抑制漂移波形成。

其中破坏气球模的解释如下：

漂移波不稳定性比如ITG模或者KBM模主要在坏曲率处出现，由涡量方程中的磁场漂移项$\epsilon\qty[r \cos \theta, f]$主导。而极向模数为$m$的磁岛改变了平行梯度：

$$\nabla_\parallel f = \nabla_{\parallel \text{eq}}f – \qty[\Psi \cos \qty(m\theta), f]$$

其中右边第一项$\nabla_{\parallel \text{eq}}$是没有磁岛的平行梯度，而$\Psi$代表磁岛宽度：$W \propto \sqrt{\Psi}$。

这进一步暗示$\epsilon\qty[r \cos \theta, f]$与$\qty[\Psi \cos \qty(m\theta), f]$存在一定的相似之处。因此在$\cos \theta \approx 1$附近的漂移波湍流通过$\cos m\theta \approx 1$的磁岛形成的磁场扰动沿着极向扩散开。这种湍流和磁岛的相互作用形成磁岛分离面的相干涡流，可通过$\qty(m, n)$稳定模式存在。

另外，带状流的振荡是由磁岛的存在引起的，磁岛通过$\qty[\Psi \cos\qty(m\theta), f]$项影响，引发磁岛诱导的测地声模GAM，这与环效应(toroidicity)$\epsilon\qty[r \cos \theta, f]$引发的GAM相对应。

磁岛附近的磁力线对扰动非常敏感，因此分离面的磁场会由于湍流扰动而变得混乱。因此也由磁岛和湍流的非线性相互作用使得总扰动增强，磁岛分离面内的湍流输运也增强。

因为相干涡流和湍流穿透进磁岛，使得磁岛的温度密度梯度下降，这在各种模拟和实验中都被观察到。

其中O点和X点的湍流扰动在磁通模拟中区别不到，但是在非磁通模拟中区别比较大。

从这个角度看，多尺度的相互作用，宏观尺度的MHD涡流通常比小尺度的湍流要强，从而导致大尺度的MHD主导湍流输运，尽管其增长率比微观湍流的增长率低。

只有当磁岛还比较小，且在增长时，小尺度的湍流才会影响到磁岛的增长。磁岛的增长率会被湍流导致的反常电流驱动增强。

---

TM稳定时

就算当撕裂模稳定或者亚稳定，湍流激发长波磁岛，在有限$\beta下$湍流扰动呈现电磁效应，形成数倍与拉莫尔半径宽的磁岛。

湍流磁场扰动导致了磁重联，也就是通过非线性作用破坏了磁面，从而形成磁岛。

这种被激发的长波磁岛也称为新经典撕裂模的种子磁岛，限制了$\beta$的进一步提升和托卡马克的高$\beta$放电。

因为新经典撕裂模是一种实验中观测到的非线性不稳定性，并在数个离子拉莫尔半径尺度上形成磁岛。

相干磁岛是由湍流引起的小尺度的磁岛合并形成。其中相干磁岛形成的具体细节分为以下三步：

1. 能量从高波数模到低波数模，通过非线性模耦合而转移。这种低波数不一定代表形成了相干磁岛。
2. 能量从扭曲对称模（如ITG，KBM和ICs）通过非线性对称混合，转移到撕裂对称模。
3. 磁重联改变了磁力线的拓扑结构，从而导致相干磁岛的形成。

磁场扰动的发展被磁岛的形成而改变，因为由湍流引起的带状流对于磁岛的演化有着很重要的影响。

所以，当等离子体是撕裂模稳定或者基本稳定时，微湍流影响了宏观的磁岛。这表示小尺度的湍流也能影响大尺度的模。这一定程度上表示了磁化等离子体的多尺度的相互作用，比如ITG模基本稳定是，ITG湍流也被ETG的湍流所影响。

---

非线性的对称性混合也是湍流（扭曲对称）形成磁岛的基础机制，尤其是在撕裂模稳定时。

这种非线性对称性混合将能量从扭曲对称的模式（如IC、ITG、KBM）向撕裂对称模式如磁岛转化。

其中扭曲对称模在线性增长阶段是对称的，但是当幅度增长到比较大时，扭曲模不再满足与非线性双流体方程，而此时撕裂对称模式确满足，因此非线性的能量就从扭曲对称模式向撕裂对称模式转化，此时磁岛就由含扭曲对称的湍流所形成。

这个激发机制分为两类：

• 由非线性的对称混合的直接激发
• 由调制对称不稳定性激发

---

相干磁岛形成的一部分机制可以归于电流的极化效应。在第6章使用静态磁岛模型，电流极化效应从湍流和磁岛的相互作用中提取了出来。

研究发现，静电交换湍流（electrostatic interchange turbulence）和静电sITG湍流（electrostatic sITG stubulence）产生的极化电流，对磁岛有去稳作用，也就是说促进磁岛激发。

通过作用于磁岛的粘滞力测量$\mu \approx 0.2 \qty[\rho^2_i \nu_\text{Ti}/ L_n]$湍流动量的扩散率可以得到有效评估。这个湍流扩散在我们使用湍流粘滞来研究托卡马克等离子体的模锁定（mode-locking）很重要，同时有效粘滞力对于计算RMP磁岛在强$E \times B$流作用下的形成也很重要。