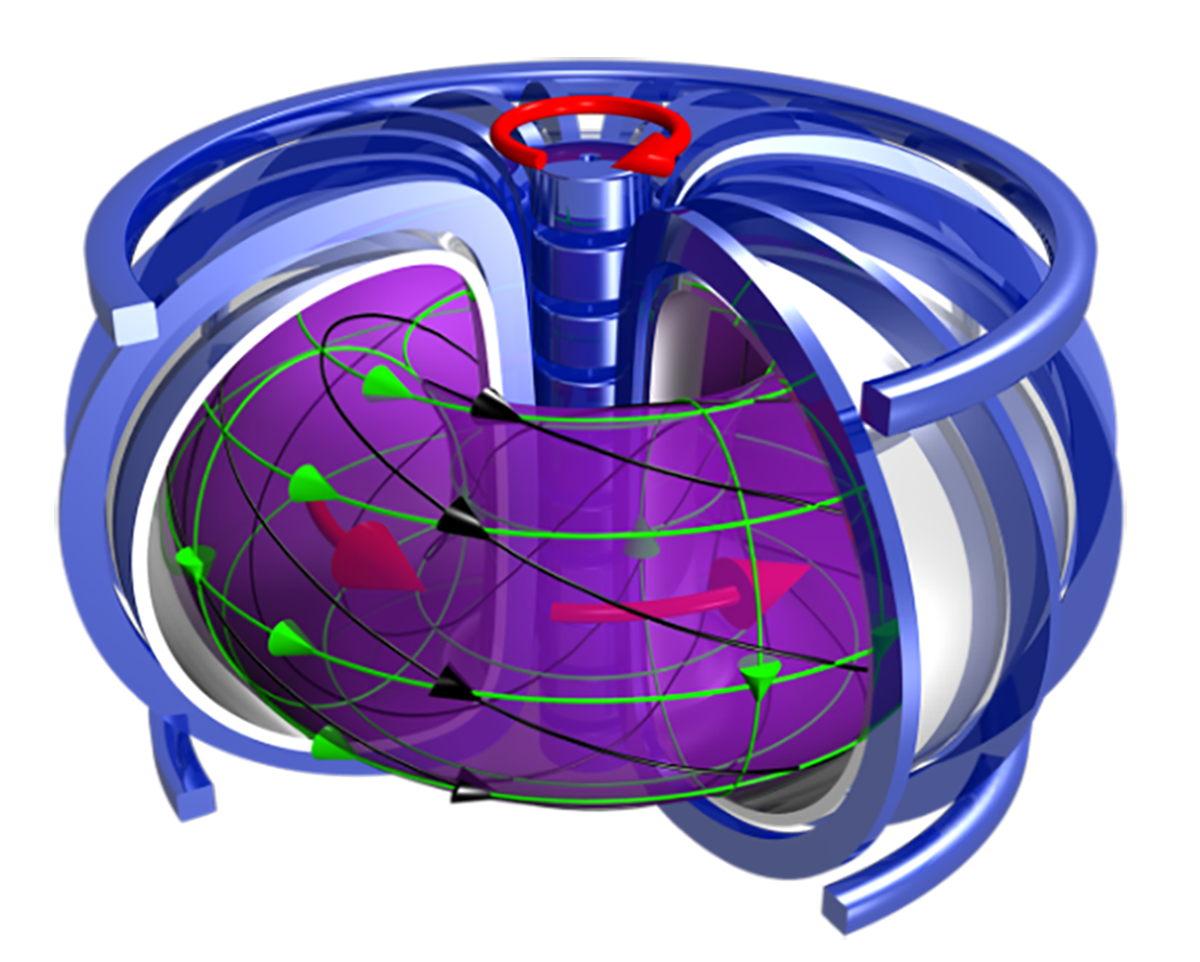
设磁面为 $\mathcal{M}$,它的一个法向量为 $\bm{n}_\mathcal{M}$。我们要求磁面函数等值面之法向量要与同一点之磁场 $\bm{B}$ 垂直,即
\begin{equation}\label{eq:磁面法向量垂直于磁场}
\begin{aligned}
\bm{n}_\mathcal{M}\dotproduct\bm{B}=0.
\end{aligned}
\end{equation}
设磁场在极向单位面积之磁通为 $\psi$,则 $\psi$ 之梯度 $\grad\psi$ 可作为它的一个法向量。我们计算 $\grad\psi$ 与 $\bm{B}$ 之内积,
\begin{equation}\label{eq:极向磁通之梯度垂直于磁场}
\begin{aligned}
\grad\psi\dotproduct\bm{B}={}&\grad\psi\dotproduct\qty(\grad\psi\crossproduct\grad\phi+F\grad\phi)
\\
={}&0+F\grad\psi\dotproduct\grad\phi
\\
={}&F\qty(\bm{e}_R\pdv{\psi}{R}+\bm{e}_Z\pdv{\psi}{Z})\dotproduct\frac{\bm{e}_\phi}{R}
\\
={}&0.
\end{aligned}
\end{equation}
由式 \eqref{eq:磁面法向量垂直于磁场} 和式 \eqref{eq:极向磁通之梯度垂直于磁场} 即可知,极向磁通 $\psi$ 确实可作为磁面函数。