电磁流体力学理论由流体三大守恒方程与麦克斯韦电磁方程组成,总共有七个方程,本文相关的线性化和本征模推导都是从这七个方程开始。
三大守恒方程和麦克斯韦方程
- 质量守恒方程
\begin{equation} \pdv{\rho}{t} + \div (\rho \bm{u}) = 0 \label{eq:fluid_mass} \end{equation}
- 动量守恒方程
\begin{equation} \rho \dv{\bm{u}}{t} + \div \bm\Pi = -\grad P + \bm{J} \cp \bm{B} \label{eq:fluid_dynamic} \end{equation}
- 能量守恒方程
\begin{equation} \dv{t}P \rho^{-\gamma} = 0 \label{eq:fluid_energy} \end{equation}
- 理想欧姆定律
\begin{equation}
\label{eq:fluid_maxwell_O}
\bm{E} = – \bm{u} \cp \bm{B}
\end{equation}
- 安培定律
\begin{equation}
\label{eq:fluid_maxwell_A}
\curl \bm{B} = \mu_0 \bm{J}
\end{equation}
- 法拉第定律
\begin{equation}
\label{eq:fluid_maxwell_F}
\curl \bm{E} = -\pdv{\bm{B}}{t}
\end{equation}
- 磁场无源
\begin{equation}
\label{eq:fluid_maxwell_B}
\div \bm{B} = 0
\end{equation}
可以看到没有使用$\div \bm{E} = \rho/\varepsilon_0$,并且安培定律忽略了电磁波动项:$\varepsilon_0\mu_0\bm{E}$。
- 忽略磁流体中的电磁波现象;
- 流体时刻处于准中性,因此由欧姆定律来代替电场散度方程。
线性化
本节内容建立在理想磁流体方程中的所有量$f=f_0+f_1$满足如下两个假设。
- $f_1 \ll f_0$ 扰动量远小于平衡量。
- $f_0 = 0$ 平衡量不参与线性方程,只有扰动量参与。
在推导过程中不考虑扰动项的二阶以上的项,可采用所有量替换成平衡量与扰动量相加之后在减去平衡量方程,或熟练后直接抄写方程时进行扰动项替代。
具体理想化假设如下:
- $\grad p_0 = 0$,均匀等离子体,无压强梯度;
- $\grad \rho_0 = 0$,等离子体密度均匀;
- $\bm{B_0} = B_0 \bm{e_z}$,平直磁场无曲率;
- $\grad B_0 = 0$,磁场强度均匀;
- $\bm{E_0} = 0$,平衡时无电场;
推导过程
守恒方程\eqref{eq:fluid_mass}的线性化
\begin{equation*}
\begin{aligned}
\pdv{\rho_1}{t} + \div \qty(\rho_0 \bm{u_1} + \rho_1 \bm{u_0}) &= 0 \\
\pdv{\rho_1}{t} + \div \qty(\rho_0 \bm{u_1}) &= 0 \\
\end{aligned}
\end{equation*}
能量方程\eqref{eq:fluid_energy}的线性化
为了方便运算,利用守恒方程将能量方程进一步推导。
\begin{equation*}
\begin{aligned}
\dv{t} p \rho^{-\gamma}
= \rho^{-\gamma}\dv{t} p – \gamma p \rho^{-\gamma – 1} \dv{t} \rho &= 0\\
\pdv{t} p + \bm{u} \cdot \grad p
– \frac{\gamma p}{\rho}
\qty(\pdv{t} \rho + \bm{u} \cdot \grad \rho) &= 0 \\
\end{aligned}
\end{equation*}
因为$\div \qty(\rho \bm{u}) = \rho \div \bm{u} + \bm{u} \cdot \grad \rho$
$$
\pdv{t} p + \bm{u} \cdot \grad p – \frac{\gamma p}{\rho}
\qty(\pdv{t} \rho + \div \qty(\rho \bm{u}) – \rho \div \bm{u}) = 0
$$
回代质量守恒方程有
\begin{equation}
\label{eq:fluid_mass_energy}
\pdv{t} p + \bm{u} \cdot \grad p
+ \gamma p
\div \bm{u} = 0
\end{equation}
进一步线性化,由于磁场压力均匀、无本体速度:
$$
\pdv{t} p_1 + \gamma p_0 \div \bm{u_1} = 0
$$
动量方程\eqref{eq:fluid_dynamic}的线性化
$$
\rho_0 \dv{t} \bm{u_1} = – \grad p_1 + \frac{1}{\mu_0}\qty(\curl \bm{B_1})\cp \bm{B_0}
$$
磁场方程\eqref{eq:fluid_maxwell_O}\eqref{eq:fluid_maxwell_F}的线性化:
$$
\pdv{t} \bm{B_1} = \curl \qty(\bm{u_1} \cp \bm{B_0})
$$
本征模
重写线性化的方程组如下
\begin{equation}
\label{eq:fluid_linear}
\begin{aligned}
&\pdv{\rho_1}{t} + \div \qty(\rho_0 \bm{u_1}) = 0 \\
&\pdv{t} p_1 + \gamma p_0 \div \bm{u_1} = 0 \\
&\rho_0 \dv{t} \bm{u_1} = – \grad p_1 + \frac{1}{\mu_0}\qty(\curl \bm{B_1})\cp \bm{B_0} \\
&\pdv{t} \bm{B_1} = \curl \qty(\bm{u_1} \cp \bm{B_0})
\end{aligned}
\end{equation}
在三维空间,方程组\eqref{eq:fluid_linear}有未知变量(扰动量)$\rho_1,\,p_1,\,\bm{u_1},\,\bm{B_1}$。
方程组可分解成八个方程与八个未知数的齐次方程。根据线性代数知识,为了使得扰动量存在非平凡解,则系数矩阵的行列式值应为0。
我们先考虑最简单的情况,即扰动$f_1$满足最简单的理想波动形式,即平面波扰动,满足如下关系式:
$$
f_1 \propto e^{-i \omega t + i \bm{k} \cdot \bm{r}}
$$
所以在计算行列式为0时,用$-iw$代替$\pdv{t}$,$i\bm{k}$代替$\grad$,可得到$\omega/k$的相关表达式。该表达式就是方程的本征模。
问题在于如何理解本征模,将$\pdv{t}$作用在方程组\eqref{eq:fluid_linear}的动量方程上,进一步化简为仅包含$\bm{u_1}$的方程如下:
$$
\rho_0 \pdv[2]{t} \bm{u_1} = \gamma p_0 \div \bm{u_1} + \frac{1}{\mu_0}\qty{\curl \qty[\curl \qty(\bm{u_1} \cp \bm{B_0})]}\cp \bm{B_0}
$$
忽略方向,仅考虑第一项压力项有声波速度$c_s^2 = \gamma p_0/\rho_0$,仅考虑第二项有阿尔芬波速度$v_A^2 = B_0^2/\mu_0 \rho_0$。
考虑方向,代入矢量表达式\eqref{eq:tensor_3},同时用$-iw$代替$\pdv{t}$,$-i\bm{k}$代替$\grad$可以得到:
\begin{equation}
\label{eq:fluid_key}
\qty(\omega^2 – v_A^2 k^2) \bm{u_1}
– c_s^2 \qty(\bm{k} \cdot \bm{u_1}) \bm{k}
+ v_A^2 k^2 \qty(\bm{u_1} \cdot \bm{b}) \bm{b}
– v_A^2 \qty[\bm{k} \cdot \qty(\bm{u_1} \cp \bm{b})]\qty(\bm{k} \cp \bm{b}) = 0
\end{equation}
上面的方程比较复杂,但是分析可得到其主要由$\bm{u_1},\, \bm{k},\, \bm{b},\, \bm{k} \cp \bm{b}$组成。
- \eqref{eq:fluid_key} $\cdot \, \bm{k}$去除$\bm{k} \cp \bm{b}$项可以得到
\begin{equation} \label{eq:fluid_ubuk1} \qty(\omega^2 – c_s^2 k^2 – v_A^2 k^2) \bm{u_1} \cdot \bm{k} + v_A^2 k^2 k_\parallel \qty(\bm{u_1} \cdot \bm{b}) = 0 \end{equation}
- \eqref{eq:fluid_key} $\cdot \, \bm{b}$去除$\bm{k} \cp \bm{b}$项可以得到
\begin{equation} \label{eq:fluid_ubuk2} \omega^2 \qty(\bm{u_1} \cdot \bm{b}) – c_s^2 k_\parallel \qty(\bm{u_1} \cdot \bm{k}) = 0 \end{equation}
方程\eqref{eq:fluid_ubuk1},\eqref{eq:fluid_ubuk2}可看做$\bm{u_1} \cdot \bm{k}$与$\bm{u_1} \cdot \bm{b}$的齐次方程组。
剪切阿尔芬波
方程组\eqref{eq:fluid_ubuk1},\eqref{eq:fluid_ubuk2}的平凡解:$\bm{u_1} \cdot \bm{k} = 0$,$\bm{u_1} \cdot \bm{b} = 0$。
如上图所示,此时$\bm{b}$与$\bm{k}$并不垂直,但扰动方向$\bm{u_1}$与传播方向$k$垂直,故此时的波动为横波。
此时方程\eqref{eq:fluid_key}变成如下形式
\begin{equation*}
\begin{aligned}
\qty(\omega^2 – v_A^2 k^2) \bm{u_1}
+ v_A^2 \qty[\qty(\bm{k} \cp \bm{b}) \cdot \bm{u_1}] \qty(\bm{k} \cp \bm{b}) &= 0 \\
\qty(\omega^2 – k_\parallel^2 v_A^2) \bm{u_1} &= 0 \\
\end{aligned}
\end{equation*}
剪切阿尔芬波(Shear Alfv\’en Wave, SAW)的色散关系就是:
$$\omega^2 – k_\parallel^2 v_A^2 = 0$$
磁声波
方程组\eqref{eq:fluid_ubuk1},\eqref{eq:fluid_ubuk2}的非平凡解$\bm{u_1} \cdot \bm{k} \neq 0$,$\bm{u_1} \cdot \bm{b} \neq 0$。
此时方程的系数矩阵的行列式值为零,可得到关于$\omega^2$的二次方程组,使用求根公式可得:
$$
\omega_\pm = \frac{1}{2} k^2 \qty(c_s^2 + v_A^2)
\qty[1 \pm \sqrt{1 – \frac{4k^2 k_\parallel^2 c_s^2 v_A^2}{\qty(k^2 c_s^2 + k^2 v_A^2)^2}}]
$$
分别对应快慢磁声波。
进一步分析,当$\bm{k} \parallel \bm{b}$ 时,有$k_\parallel = k$,计算可得此时快慢磁声波可以进一步化简,其中一支退化成阿尔芬波。
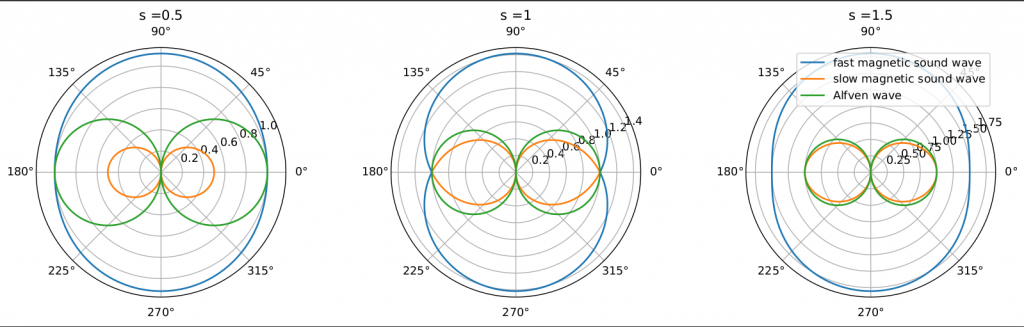
上图为三支声波在与$\bm{k}$与$\bm{b}$不同角度时的三只本征模的波速,其中$s$表示根号下两个值的比值。
相关矢量表达式
\begin{equation}
\label{eq:tensor_1}
\bm{A} \cdot \bm{B} \cp \bm{C} =
\bm{C} \cdot \bm{A} \cp \bm{B} =
\bm{B} \cdot \bm{C} \cp \bm{A}
\end{equation}
\begin{equation}
\label{eq:tensor_2}
\div \qty(\curl \bm{A}) =
\curl \qty(\grad u) = 0
\end{equation}
\begin{equation}
\label{eq:tensor_3}
\qty(\bm{A} \cp \bm{B}) \cp \bm{C} =
\qty(\bm{A} \cdot \bm{C})\bm{B} –
\qty(\bm{B} \cdot \bm{C})\bm{A}
\end{equation}
\begin{equation}
\label{eq:tensor_4}
\bm{B} \cdot \curl \bm{A} =
\div \qty(\bm{A} \cp \bm{B})
+ \bm{A} \cdot \curl \bm{B}
\end{equation}
\begin{equation}
\label{eq:tensor_5}
\curl \qty(\bm{a} \cp \grad b)
= \qty(\div \grad b) \bm{a} – \grad b \qty(\div \bm{a})
+ \grad b \cdot \grad \bm{a} – \bm{a} \cdot \grad \grad b
\end{equation}

